Abertura Numérica e Resolução

por **Admin** Qui Mar 10, 2022 9:03 pm

Introdução

A abertura numérica de uma objetiva de microscópio é a medida de sua capacidade de coletar luz e resolver detalhes finos da amostra enquanto trabalha a uma distância fixa do objeto (ou amostra). Ondas de luz formadoras de imagem passam pela amostra e entram na objetiva em um cone invertido, conforme ilustrado na Figura 1(a). A luz branca consiste em um amplo espectro de ondas eletromagnéticas, cujos períodos variam entre 400 e 700 nanômetros. Como referência, é importante saber que 1 milímetro equivale a 1000 micrômetros e 1 micrômetro equivale a 1000 nanômetros. A luz de cor verde tem uma faixa de comprimento de onda centrada em 550 nanômetros, o que corresponde a 0,55 micrômetros. Se pequenos objetos (como um espécime manchado típico montado em uma lâmina de microscópio) são vistos através do microscópio, a luz incidente nesses objetos diminutos é difratada de modo que se desvie da direção original (Figura 1(a)). Quanto menor o objeto, mais pronunciada será a difração dos raios de luz incidentes. Valores mais altos de abertura numérica permitem que raios cada vez mais oblíquos entrem na lente frontal objetiva, o que produz uma imagem mais bem resolvida e permite que estruturas menores sejam visualizadas com maior clareza. Ilustrado na Figura 1(a) está um sistema de microscópio simples que consiste em uma objetiva e uma amostra sendo iluminadas por um feixe de luz colimado, o que seria o caso se nenhum condensador fosse usado. A luz difratada pelo corpo de prova é apresentada como um cone invertido de meio ângulo ( mais pronunciada será a difração dos raios de luz incidentes. Valores mais altos de abertura numérica permitem que raios cada vez mais oblíquos entrem na lente frontal objetiva, o que produz uma imagem mais bem resolvida e permite que estruturas menores sejam visualizadas com maior clareza. Ilustrado na Figura 1(a) está um sistema de microscópio simples que consiste em uma objetiva e uma amostra sendo iluminadas por um feixe de luz colimado, o que seria o caso se nenhum condensador fosse usado. A luz difratada pelo corpo de prova é apresentada como um cone invertido de meio ângulo ( mais pronunciada será a difração dos raios de luz incidentes. Valores mais altos de abertura numérica permitem que raios cada vez mais oblíquos entrem na lente frontal objetiva, o que produz uma imagem mais bem resolvida e permite que estruturas menores sejam visualizadas com maior clareza. Ilustrado na Figura 1(a) está um sistema de microscópio simples que consiste em uma objetiva e uma amostra sendo iluminadas por um feixe de luz colimado, o que seria o caso se nenhum condensador fosse usado. A luz difratada pelo corpo de prova é apresentada como um cone invertido de meio ângulo ( Ilustrado na Figura 1(a) está um sistema de microscópio simples que consiste em uma objetiva e uma amostra sendo iluminadas por um feixe de luz colimado, o que seria o caso se nenhum condensador fosse usado. A luz difratada pelo corpo de prova é apresentada como um cone invertido de meio ângulo ( Ilustrado na Figura 1(a) está um sistema de microscópio simples que consiste em uma objetiva e uma amostra sendo iluminadas por um feixe de luz colimado, o que seria o caso se nenhum condensador fosse usado. A luz difratada pelo corpo de prova é apresentada como um cone invertido de meio ângulo (α ), que representa os limites de luz que podem entrar na objetiva. Para aumentar a abertura efetiva e o poder de resolução do microscópio, um condensador (Figura 1(b)) é adicionado para gerar um cone de raios no lado da iluminação da amostra. Isso permite que a objetiva colete raios de luz resultantes de ângulos de difração maiores, aumentando a resolução do sistema do microscópio. A soma dos ângulos de abertura da objetiva e do condensador é chamada de abertura de trabalho . Se o ângulo de abertura do condensador corresponder ao objetivo, a resolução máxima será obtida.

Para permitir comparar duas objetivas e obter um controle quantitativo da resolução, a abertura numérica ou a medida do ângulo sólido coberto por uma objetiva é definida como:

Abertura Numérica (NA) = η • sin (α) (1)

onde α é igual à metade do ângulo de abertura da objetiva e η é o índice de refração do meio de imersão usado entre a objetiva e a lamínula que protege a amostra (η = 1 para ar; η = 1,51 para óleo ou vidro). Ao examinar a Equação (1), é evidente que o índice de refração é o fator limitante na obtenção de aberturas numéricas maiores que 1,0. Portanto, a fim de obter maiores aberturas numéricas de trabalho, o índice de refração do meio entre a lente frontal da objetiva e a lamínula da amostra deve ser aumentado. A maior abertura angular obtida com uma objetiva de microscópio padrão seria teoricamente de 180 graus, resultando em um valor de 90 graus para o meio ângulo usado na equação de abertura numérica. O seno de 90 graus é igual a um, o que sugere que a abertura numérica é limitada não apenas pela abertura angular, mas também pelo índice de refração do meio de imagem. Praticamente, ângulos de abertura superiores a 70 a 80 graus são encontrados apenas nas objetivas de mais alto desempenho que normalmente custam milhares de dólares.

A resolução de um microscópio óptico é definida como a menor distância entre dois pontos em uma amostra que ainda pode ser distinguida como duas entidades separadas. A resolução está diretamente relacionada à ampliação útil do microscópio e ao limite de percepção dos detalhes da amostra, embora seja um valor um tanto subjetivo em microscopia porque em alta ampliação, uma imagem pode parecer fora de foco, mas ainda ser resolvida com a capacidade máxima do objetiva e componentes ópticos auxiliares. Devido à natureza ondulatória da luz e à difração associada a esses fenômenos, a resolução de uma objetiva de microscópio é determinada pelo ângulo das ondas de luz que são capazes de entrar na lente frontal e, portanto, o instrumento é considerado limitado à difração .. Este limite é puramente teórico, mas mesmo uma objetiva teoricamente ideal sem erros de imagem tem uma resolução finita.

Os observadores perderão nuances finas na imagem se a objetiva projetar detalhes no plano intermediário da imagem que são menores do que o poder de resolução do olho humano (uma situação típica em ampliações baixas e aberturas numéricas altas). O fenômeno da ampliação vazia ocorrerá se uma imagem for ampliada além do poder de resolução física das imagens. Por essas razões, a ampliação útil para o observador deve ser otimamente superior a 500 vezes a abertura numérica da objetiva, mas não superior a 1.000 vezes a abertura numérica.

voltar ao topo ^Mídia de imersão

Uma forma de aumentar o poder de resolução óptica do microscópio é usar líquidos de imersão entre a lente frontal da objetiva e a lamínula. A maioria das objetivas na faixa de ampliação entre 60x e 100x (e superior) são projetadas para uso com óleo de imersão. Bons resultados foram obtidos com óleo com índice de refração de n = 1,51, que foi precisamente ajustado ao índice de refração do vidro. Todas as reflexões no caminho do objeto ao objetivo são eliminadas desta forma. Se esse truque não fosse usado, a reflexão sempre causaria perda de luz na lamínula ou na lente frontal no caso de grandes ângulos (Figura 2).

A abertura numérica útil da objetiva e, portanto, o poder de resolução seriam reduzidos pela reflexão descrita acima. A abertura numérica de uma objetiva também depende, até certo ponto, da quantidade de correção para a aberração óptica. Objetivas altamente corrigidas tendem a ter aberturas numéricas muito maiores para a respectiva ampliação, conforme ilustrado na Tabela 1.

Abertura Numérica Objetiva versus Correção Óptica

O disco Airy e a resolução do microscópio

Quando a luz dos vários pontos de um espécime passa pela objetiva e é reconstituída como uma imagem, os vários pontos do espécime aparecem na imagem como pequenos padrões (não pontos) conhecidos como padrões Airy. Esse fenômeno é causado pela difração ou dispersão da luz à medida que ela passa pelas partes e espaços minúsculos da amostra e pela abertura circular traseira da objetiva. O limite até o qual dois pequenos objetos ainda são vistos como entidades separadas é usado como medida do poder de resolução de um microscópio. A distância em que esse limite é atingido é conhecida como resolução efetiva do microscópio e é denotada como d ₀. A resolução é um valor que pode ser derivado teoricamente dados os parâmetros ópticos do instrumento e o comprimento de onda médio de iluminação.

É importante, antes de tudo, saber que a objetiva e a lente do tubo não captam a imagem de um ponto no objeto (por exemplo, um orifício minúsculo em uma folha de metal) como um disco brilhante com bordas bem definidas, mas como um mancha cercada por anéis de difração, chamados discos de Airy (veja a Figura 3(a)). As representações tridimensionais do padrão de difração próximo ao plano de imagem intermediário são conhecidas como função de espalhamento de pontos (Figura 3(b)). Um disco de Airy é a região delimitada pelo primeiro mínimo do padrão de airy e contém aproximadamente 84 por cento da energia luminosa, conforme ilustrado na Figura 3(c). A função point-spread é uma representação tridimensional do disco Airy.

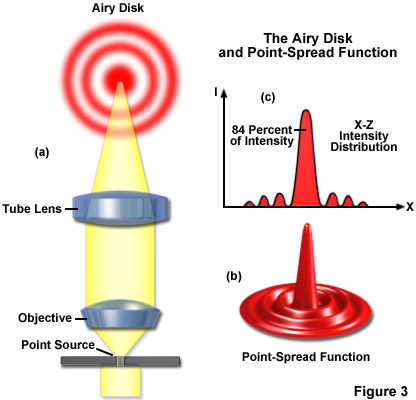
Abertura Numérica e Resolução Resolutionfigure3

A resolução pode ser calculada de acordo com a famosa fórmula introduzida por Ernst Abbe no final do século XIX e representa uma medida da nitidez da imagem de um microscópio de luz:

Resolução _{x, y} = λ / 2 [η • sen (α)] (2) Resolução _z = 2λ / [η • sen (α)] ²(3)

onde λ é o comprimento de onda da luz, η representa o índice de refração do meio de imagem como descrito acima, e o termo combinado η • sin(α) é conhecido como abertura numérica objetiva ( NA ). As objetivas comumente usadas em microscopia têm uma abertura numérica menor que 1,5, restringindo o termo α nas Equações (2) e (3)para menos de 70 graus (embora os novos objetivos de alto desempenho se aproximem desse limite). Portanto, o limite teórico de resolução no menor comprimento de onda prático (aproximadamente 400 nanômetros) é de cerca de 150 nanômetros na dimensão lateral e aproximando-se de 400 nanômetros na dimensão axial quando se utiliza uma objetiva com abertura numérica de 1,40. Assim, estruturas que estão mais próximas que essa distância não podem ser resolvidas no plano lateral usando um microscópio. Devido ao significado central da inter-relação entre o índice de refração do meio de imagem e a abertura angular da objetiva, Abbe introduziu o conceito de abertura numérica durante a explicação da resolução do microscópio.

Os anéis de difração no disco de Airy são causados pela função limitante da abertura da objetiva, de modo que a objetiva atua como um orifício, atrás do qual se encontram os anéis de difração. Quanto maior a abertura da objetiva e do condensador, menor será o d ₀ . Assim, quanto maior a abertura numérica do sistema total, melhor a resolução. Uma das várias equações relacionadas à fórmula original de Abbe que foram derivadas para expressar a relação entre abertura numérica, comprimento de onda e resolução é:

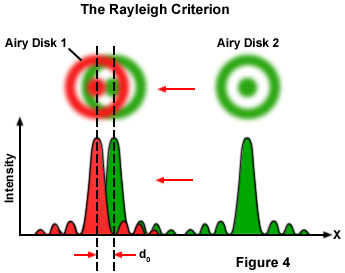
Resolution_x,y or d₀ = 1.22λ / [NA_Obj + NA_Con](4)

Onde λ é o comprimento de onda de imagem da luz, NA _Con é a abertura numérica do condensador e NA _Obj é igual à abertura numérica objetiva. O fator 1,22foi retirado do cálculo para o caso ilustrado na Figura 4 para a aproximação de dois discos de Airy onde os perfis de intensidade foram sobrepostos. Se os dois pontos da imagem estiverem distantes um do outro, eles serão facilmente reconhecidos como objetos separados. No entanto, quando a distância entre os discos de Airy é cada vez menor, um ponto limite é alcançado quando o máximo principal do segundo disco de Airy coincide com o primeiro mínimo do primeiro disco de Airy. Os perfis sobrepostos exibem dois máximos de brilho separados por um vale. A intensidade no vale é reduzida em aproximadamente 20% em comparação com os dois máximos. Isso é apenas suficiente para o olho humano ver dois pontos separados, um limite que é referido como o critério de Rayleigh .

Abertura Numérica e Resolução Resolutionfigure4

Uma comparação pode ajudar a tornar isso mais fácil de entender. É muito improvável que um cabo telefônico seja usado para a transferência eletrônica do delicado som de um violino, já que a largura de banda desse meio é muito restrita. Resultados muito melhores são obtidos se forem usados microfones e amplificadores de alta qualidade, cuja faixa de frequência é idêntica à faixa de audição humana. Na música, a informação está contida nas frequências sonoras médias; no entanto, as nuances finas do som estão contidas nos tons altos. No microscópio, as sutilezas de uma estrutura são codificadas na luz difratada. Se você quiser vê-los no espaço de imagem atrás da objetiva, você deve certificar-se de que eles são primeiro reunidos pela objetiva. Isso se torna mais fácil com um ângulo de abertura mais alto e, portanto, uma abertura numérica aumentada.

A abertura numérica das objetivas aumenta com a ampliação até cerca de 40x (ver Tabelas 1 e 2), mas se estabiliza entre 1,30 e 1,40 (dependendo do grau de correção de aberração) para versões de imersão em óleo. Na Tabela 2 são apresentados os valores calculados para a resolução de objetivos tipicamente utilizados em laboratórios de pesquisa e ensino. A resolução ponto a ponto na amostra, d ₀ , está listada na tabela junto com o tamanho ampliado da imagem ( D ₀ ) no plano intermediário da ocular (usando luz verde de comprimento de onda de 550 nanômetros). Também na tabela, o valor n representa o número de pixels resolvidos se eles estiverem organizados em uma matriz linear ao longo do diâmetro de campo de 20 milímetros (20 milímetros/D ₀).

Resolução para Objetivos Selecionados

Objective/NA	d ₀ (μm)	D ₀ (μm)	n
0,5x / 0,15	2.2	11.2	1786
10x / 0,30	1.1	11.2	1786
20x / 0,50	0.7	13.4	1493
40x / 0,75	0.45	17.9	1117
40x / 1,30 (óleo)	0.26	10.3	1942
63x / 1,40 (óleo)	0.24	15.1	1325
100x / 1,30 (óleo)	0.26	25.8	775

Você não deve tentar aumentar a ampliação geral de um microscópio usando oculares que forneçam uma ampliação adicional alta (por exemplo, 16x, 20x ou 25x) ou outros pós-combustores ópticos se a objetiva não fornecer pixels suficientes em uma abertura numérica baixa. Por outro lado, você perderá nuances sutis se a objetiva projetar detalhes muito finos na imagem intermediária e você estiver usando uma ocular com baixa ampliação. Para observar detalhes finos da amostra no microscópio óptico, as características diminutas presentes na amostra devem ter contraste suficiente e projetar uma imagem intermediária em um ângulo um pouco maior que o poder de resolução angular do olho humano. Como mencionado anteriormente, a ampliação total combinada (objetiva e ocular) de um microscópio deve ser superior a 500x, mas menos de 1000x a abertura da objetiva. Esse valor é conhecido comoalcance da ampliação útil .
Nas observações de rotina do dia-a-dia, muitos microscopistas não tentam alcançar a maior resolução de imagem possível com seus equipamentos. O poder de resolução de um microscópio é a característica mais importante do sistema óptico e influencia a capacidade de distinguir detalhes finos de uma amostra em particular. O fator primário na determinação da resolução é a abertura numérica objetiva, mas a resolução também depende do tipo de amostra, coerência de iluminação, grau de correção de aberração e outros fatores, como metodologia de aprimoramento de contraste no sistema óptico do microscópio ou no próprio exemplar.