Processamento de imagem em Microscópios Confocais

procimagem02

Importante !!! O objetivo desta nota experimental, é  somente facilitar o procedimento experimental no laboratório. Para a preparação da atividade, relatório e seminário não deixe de consultar a bibliografia sugerida.

Sem dúvida este é o século da imagem. O desenvolvimento da televisão, satélites, sistemas de espionagem, exames médicos (raios – X, ultra-sonografia, tomografias,  ressonância magnética, etc.) e por último a popularização dos computadores, modificam nosso conceito de obtenção e visualização da informação.

Mais recentemente as técnicas de obtenção de imagens ( DVD, Scanners, cintiladores, etc.) juntamente com uma melhora dos pacotes computacionais gráficos, permiti-nos uma análise de informações muito mais rápida e precisa e em muitos casos conclusões que tornaram-se possíveis somente depois da utilização de técnicas gráficas.

Dentro deste contexto mundial, as técnicas de processamento de imagens constituem importante ferramenta em inúmeras áreas. Estas técnicas permitem o tratamento de dados visuais, possibilitando a busca pela informação desejada.

Nesta atividade estudaremos a técnica de processamento de imagem através da transformada de Fourier da imagem. Analisando a imagem no espaço recíproco de freqüências espaciais, é possível identificar e filtrar partes da imagem

.

Se posicionarmos uma fonte pontual ao longo de um plano focal de uma lente positiva, a imagem da fonte pontual ocorre no infinito. O inverso também é verdade. Devido ao fato do plano focal, e um plano focal no infinito serem conjugados, parece plausível que as lentes formariam uma imagem de um padrão de difração a campo distante em seu plano focal.

Examinando como uma lente processa uma onda plana, vamos observar que a transformação é equivalente à transformada de Fourier.

Utilizando uma representação mais intuitiva, é possível demonstrar que o ângulo de incidência de uma onda plana é mapeado numa única posição espacial atrás do plano focal de uma lente. Esta demonstração pode ser feita por óptica geométrica, sendo possível mostrar que uma lente, com uma fonte pontual de seu eixo, mas em seu plano focal é uma função do ângulo pelo qual a onda plana faz com o eixo óptico da lente.

.

Em 1871, enquanto desenvolvia uma teoria de microscópio para Carl Zeiss, Abbe apresentou uma visão de imagem coerente que levou para o campo da óptica chamado Processamento de Sinal Óptico. A teoria de Abbe assume que a imagem de um objeto pode ser decomposto em um número de grãos elementares, cada um difrata luz em um certo ângulo que é uma função do período dos grãos e suas orientações.

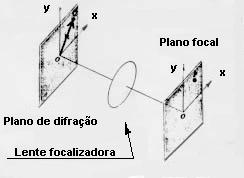
proc1Fig.6.1 – Objeto no plano de difração.

O fluxo de luzes difratadas são ondas planas. As formas dos padrões de difração são determinadas pela abertura da lente utilizada. Os padrões de difração funcionam como fontes de onda que se propagam, do plano focal ao plano de imagem onde interferem para produzir a imagem.

Uma vez que a teoria de Abbe foi desenvolvida, muitas aplicações no campo de processamento de sinal foram feitas. Todas se baseiam na premissa de que a transformada de Fourier do objeto esta presente no plano focal frontal da lente. Esta é uma das duas ideias básicas da teoria de Abbe. Decompõe-se a luz de um objeto em um grupo de ondas planas que são focalizadas em discos de Airy (Assumindo que a abertura limitante é circular) no plano focal frontal. A localização de um disco de Airy no plano focal é uma função do ângulo pelo qual a onda plana faz com o eixo óptico.

A segunda ideia fundamental contida na teoria de Abbe é que cada disco de Airy age como uma fonte produzindo uma onda esférica. Estas interferem no plano da imagem para produzir a imagem do objeto.

A teoria de Abbe permite-nos tratar o problema do processamento de imagens como uma difração de Fraunhofer. Pela fig.6.1 podemos considerar o objeto iluminado como sendo uma abertura no plano de difração – as características de tal objeto são dadas pela função de transmissão de luz g(x,y). Após os raios difratados atravessarem a lente, eles serão focalizados no plano focal XY .

Uma Segunda lente (após a primeira) com plano focal na mesma posição da anterior transforma o padrão de difração de volta na imagem do objeto.

Se uma barreira é colocada no plano de Fourier, algumas frequências espaciais serão perdidas e a imagem posteriormente formada perde definição e/ou é modificada.

É importante dizer que na verdade a imagem formada tem definição menor que a do objeto, já que as lentes não são infinitas e as frequências mais altas são sempre perdidas. Mas como as frequências mais altas possuem intensidade menor, se as lentes forem muito grandes, a imagem será praticamente igual ao objeto.

.

.

É de conhecimento geral que o Laser conserva sua coerência através de uma distância relativamente grande, não estando sujeito portanto às limitações associadas às fontes incoerentes em geral.

O Laser gera frentes de onda bastante definidas, o que permite uma maior facilidade em se operar opticamente com ele, além de ser extremamente monocromático.

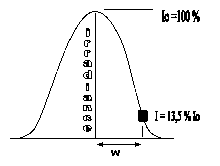
proc2

Fig.6.2 – Perfil de irradiação do Laser.

O Laser que usaremos em nosso experimento é um Laser de He-Ne que opera no modo TEM (Transversal Eletromagnetic) com uma frente de onda plana e um feixe cujo perfil é uma gaussiana ou quase ( Não esquecer dos ruídos).

.

proc3

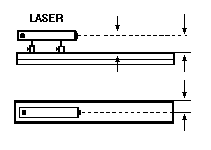
Fig. 6.3 – Alinhamento do Laser.

Antes de iniciar o experimento é necessário testar o alinhamento do feixe de Laser em relação ao trilho óptico.

Isto é possível, percorrendo o trilho com um diafragma todo fechado em um suporte apropriado, deve-se desloca-lo em todo o trilho e observar se a luz sempre esta na mesma posição, depois dando um giro de 180o em relação ao eixo do suporte, fazer novamente o mesmo teste, veja fig.6.3

.

Para podermos iniciar o experimento, precisaremos “trabalhar” a luz do Laser para que possa ficar em condições de ser utilizada continuamente ao longo do trilho óptico.

O Laser He-Ne é muito utilizado no alinhamento de sistemas ópticos , devido à pequena divergência angular do feixe.

Normalmente os elementos ópticos são alinhados na direção do feixe incidente, simplesmente observando se o elemento esta centrado no feixe, e se o feixe refletido e/ou transmitido esta centrado com a direção de incidência. Este é um ajuste preliminar muito útil (fig. 6.4).

proc4

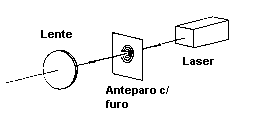
Fig.6.4 – Ajuste preliminar do alinhamento.

proc5

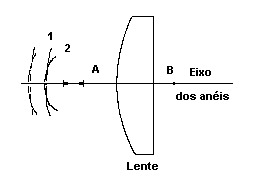
Fig. 6.5 – Ajuste interferométrico do alinhamento.

Depois deste primeiro ajuste, usamos um método interferométrico muito preciso para alinhamento de sistemas ópticos que consiste na montagem abaixo.

Quando uma frente de onda plana atravessa uma lente, duas frentes de ondas esféricas são refletidas pela primeira e segunda superfícies da lente.

As duas frentes de onda coerentes, com curvaturas diferentes, interferem gerando um padrão de anéis de interferência. O que vemos no anteparo são anéis de interferência e uma mancha luminosa devido à diferença de intensidade dos dois feixes refletidos pela lente (fig. 6.6).

proc6

Fig. 6.6 – Figuras de interferência no alinhamento.

A direção do eixo dos anéis depende do ângulo entre o feixe incidente e o eixo óptico da lente, enquanto que a mancha luminosa refletida caracteriza o ponto onde o feixe incide na lente.

Quando a mancha luminosa e os anéis de interferência estão centrados no orifício do anteparo, a direção do feixe incidente esta coincidindo com o eixo óptico, e com o centro da lente.

.

Se posicionarmos uma abertura no plano de frequências, esta restringira a máxima frequência que passa através do sistema. Esta abertura atua como um filtro passa baixa.

Uma aplicação frequente da filtragem espacial, é o uso de uma abertura circular para suavizar o feixe de um Laser. O modo fundamental do Laser é uma onda gaussiana, porém devido à imperfeições e ruídos temos uma gaussiana adicionada à ruídos (fig. 6.7).

Essas imperfeições são atenuadas quando posicionamos o plano focal de uma lente de comprimento focal f de uma abertura com um diâmetro de aproximadamente lf/r , eliminaremos as flutuações das frequências espaciais altas e geraremos um feixe mais próximo do ideal.

proc7

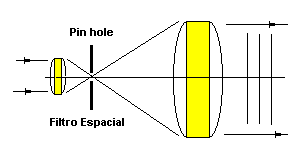
Fig.6.7 Montagem do filtro espacial.

Variando-se a posição objetiva em relação ao pinhole, pode-se ver projetado no anteparo, figuras de difração circular, o que permite calcular através da difração, o diâmetro do furo.

.

Após o sistema todo alinhado, expandido, e filtrado, precisamos colima-lo ou seja torná-lo paralelo para que não seja divergente, e com isso podermos projetar as imagens para a demonstração – Fig. 6.8

proc8

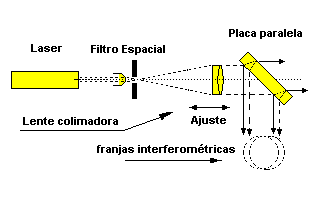
Fig.6.8 – Ajuste do colimador através das franjas de interferência.

Vamos usar uma técnica simples que permite obter excelentes resultados. Na frente da lente colimadora, colocaremos uma placa de vidro de faces planas e paralelas como na fig.6.8 , sendo que as reflexões que o feixe irá sofrer na primeira face e segunda face nos dão uma figura de interferência

Deslocando-se a lente colimadora , observa-se a figura de interferência até que as franjas mudem de direção ( fato que só vai ocorrer quando o feixe de luz estiver paralelo).

.

A fig.6.9 será utilizada para explicar a aplicação da teoria de Abbe . Ha três lentes na figura, mas a primeira esta presente somente para produzir uma onda plana para iluminar o objeto.

proc9

Supondo que as outras lentes tenham a mesma distância focal e fazendo a magnificação do sistema unitária. O plano objeto para as duas lentes esta no plano focal frontal de L1 e o plano imagem esta no plano focal posterior de L2 . A lente L1 produz uma transformada de Fourier do objeto no plano F, chamado de plano de frequência. A distribuição de luz no plano de frequência funciona como a fonte para L2 , que produz a transformada do plano de frequência no plano I (plano imagem) . Assim a distribuição no plano I é a transformada de Fourier da transformada de Fourier do objeto. Esta é a imagem do objeto.

Agora se modificarmos a distribuição de luz no plano F, por exemplo inserindo uma abertura neste plano com o eixo dela alinhado com o eixo óptico do sistema . Se o tamanho da abertura é tão pequeno que permite somente uma parte infinitesimal da imagem passar, esta se comportará como uma fonte pontual colocada no plano focal de L2 , logo a imagem em I será uma onda plana.

Na montagem vamos projetar duas imagens superpostas, o símbolo da Unicamp e uma rede. A transformada da rede é um padrão com simetria parecida com uma estrutura cristalina planar, em cada ponto do padrão está toda a informação do emblema. Desta forma, a interrupção de todos os pontos, exceto um, leva à formação em I, somente do emblema, sem a rede.

.

a) Alinhamento do feixe de Laser sobre o trilho (deslocando-se um furo sobre o trilho este deve ser sempre iluminado).

b) Montagem de um sistema expansor de feixe (Usar objetiva de microscópio).

c) Montagem do Pin-hole e alinha-lo até conseguir a Filtragem Espacial.

d) Através da figura de difração calcular a abertura do Pinhole.

e) Montagem da placa paralela para ajuste do colimador.

f) Montagem do carrossel de fendas.

g) Montagem das lentes p/ a dupla transformada.

h) Montagem dos slides e conseqüente observação:

Separar imagens superpostas com redes de forma a obter só a imagem ou só a rede.

Separar redes com orientações diferentes.

Mudar o período da imagem de redes através da seleção das ordens de difração no plano de Fourier, etc.

.

-Goodman, J.W.,”Introduction to Fourier Optics“, McGraw – Hill Book Company

-Guenther, Robert, “Modern Optics“, John Wiley&Sons

Oliveira, E. A. et al : “Alinhamento Interferométrico de Sistemas Ópticos” ,

Revista de Física Aplicada e Instrumentos ,1, 1985.

– Jenkins, F. A. and White, H. E. : “Fundamentals of Optics“.

– Malacara, D., “Optical Shep Testing“.

– Gabor, D., “Microscopy of reconstructed wave-fronts“, Proc. Roy. Soc. A vol.197.

– Lipson, H., “Optical Transforms“.

– Bugnan, J.G. e J. L. Thompson, “An interference method for determining the degree of paralelism of surfaces“. Apl. Optics(7) 5, 1968.

– Meyer-Arendt, J. R.,”Introduction to classical and modern optics“.

.

Sites da Internet:

http://www.scioncorp.com/frames/fr_download_now.htm

http://www.microsoft.com/directx/download.asp?RLD=51

http://www.cs.unm.edu/~brayer/vision/fourier.html

.

5 – Apêndice : Fotos

proc10

Fig. 6.10 – Imagem

proc11

Fig. 6.11 – Transformada da imagem ant.

proc12

Fig. 6.12 – Imagem

proc13

Fig. 6.13 – Transformada da imagem ant.

proc14

Fig. 6.14 – Imagem

proc15

Fig. 6.15 – Transformada da imagem ant.

proc16

Fig. 6.16 – Imagem

proc17

Fig. 6.17 – Transformada da imagem ant.